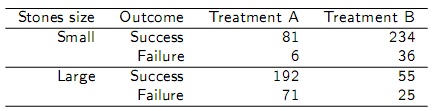
از جمله آزمون های مورد استفاده برای مقایسه دو متغیر کیفی مستقل، آزمون منتل هانزل می باشد. به عنوان مثال فرض کنید می خواهیم توانایی دو روش درمانی برای رفع سنگ کلیه را مورد بررسی قرار دهیم. بیماران مورد نظر برحسب اندازه ی سنگ کلیه و موفق یا ناموفق بودن روش درمانی به صورت جدول زیر دسته بندی می شوند.

در حالت کلی اگر ترکیب جدول 2*2 در i امین طبقه به شکل زیر باشد:

برای تهیه آماره مورد نظر فرض کنید k طبقه متوالی از جدول 2*2 توافقی وجود دارد و در طبقه i ام ، P₁ ⁱ احتمال رخداد رده اول (موفقیت) در i امین طبقه و ، P₂ ⁱ احتمال رخداد رده دوم (شکست) در i امین طبقه باشد، می خواهیم فرض استقلال دو متغیر را مورد بررسی قرار دهیم.

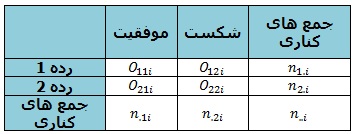
فرض معادل برای این منظور به صورت، H₀ : P₁ⁱ=P₂ⁱ را برای i=1,…,k  آزمون کنیم آماره آزمون منتل هانزل به صورت زیر تعریف می شود:

O_11i از توزیع فوق هندسی پیروی می کند و در رابطه فوق داریم :

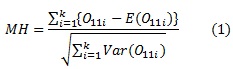
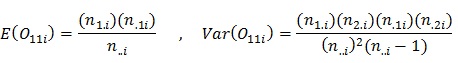
به این ترتیب با در نظر گرفتن Z_α عنوان مقدار حاصل از جدول توزیع نرمال استاندارد در سطح α، برای انجام آزمون، اگر فرض مقابل به شکل  H₁ : P₁ⁱ>P₂ⁱ تعریف شود، فرض صفر را در سطح خطای α نمی پذیریم اگر MH ≥ Z_α .

چنانچه فرض مقابل به شکلH₁ : P₁ⁱ< P₂ⁱ تعریف شود، MH ≤ -Z_α بیانگر عدم تأیید فرض صفر می باشد. به عنوان آخرین حالت اگر فرض مقابل دو طرفه باشد، فرض صفر در سطح خطای α پذیرفته نمی شود  اگر MH|≥ Z_{α/2 |}  باشد.

مثال

فرض کنید 3 جدول با ترکیب زیر در اختیار داریم :

مقدار آماره منتل هانزل با استفاده از رابطه (1) برابر 0.895 حاصل می شود. با در نظر گرفتنα=0.05 ، مقدار حاصل از جدول توزیع نرمال استاندارد برابر 1.96 خواهد بود. حال اگر فرض مقابل دوطرفه را مدنظر قرار دهیم، 1.96> 0.895 بوده و فرض صفر مبنی بر یکسان بودن نتایج سه جدول ارائه شده رد نمی شود. به عبارت دیگر نسبت موفقیت ها و شکست ها در سه جدول فوق یکسان است.

منبع : مقدمه ای بر روش های آماری ناپارامتری / نوشته : اکبر گلدسته / انتشارات جهاد دانشگاهی / 1390.

براي مشاهده ساير مقاله هاي تحليل آماري اين وب سايت بر لينک زير کليک نماييد: صفحه مقاله هاي تحليل آماري