در میان روش های نمونه گیری با احتمالات برابر، روش نمونه گیری تصادفی ساده یکی از ساده ترین و قدیمی ترین روش های نمونه گیری است که در عمل کاربرد بسیاری دارد.

تعریف نمونه گیری تصادفی ساده

به تصویر بالای این صفحه نگاه کنید. برگه های کوچک و یکسانی، حاوی نام اشخاص، را داخل کلاه انداخته و پس از تکان دادن کلاه اقدام به انتخاب چند برگه کنیم.

اگر نمونه ای به حجم n  از جامعه ای به حجم N  به گونه ای انتخاب شود که هر نمونه ی ممکن n تایی شانس یکسان برای انتخاب شدن داشته باشد، آن را نمونه گیری تصادفی ساده می نامند.

نمونه گیری تصادفی ساده به دو روش نمونه گیری با جایگذاری و نمونه گیری بدون جایگذاری قابل اجرا می باشد اما در عمل نمونه گیری با جایگذاری کاربرد چندانی ندارد .

 در نمونه گیری تصادفی بدون جایگذاری، احتمال انتخاب تمام   نمونه ی ممکن یکسان بوده و برابر  می باشد . همچنین ثابت می شود که احتمال قرار گرفتن هر واحد جامعه در نمونه برابر  است.

1- برآورد میانگین جامعه

هدف از بررسی نمونه ای استنباط کردن درباره ی جامعه بر مبنای اطلاعات موجود در نمونه است و یک راه برای استنباط، برآورد کردن بعضی از پارامترهای جامعه با استفاده از مشاهدات نمونه می باشد. هدف بررسی نمونه ای اغلب برآورد میانگین و مقدار کل جامعه است.

بنابراین در ادامه به معرفی این مقادیر می پردازیم. با تعریف واحدهای جامعه به صورت   و قراردادن  به عنوان واحدهای نمونه ی انتخاب شده ثابت می شود که  یک برآوردگر نااریب برای میانگین جامعه یعنی   است .

مقدار  به تنهایی اطلاعات کمی درباره میانگین جامعه در اختیار ما قرار می دهد، برای آنکه بتوانیم مناسب بودن برآوردگر خود را ارزیابی کنیم واریانس آن را بدست می آوریم. واریانس این برآوردگر نیز به صورت زیر بدست می آید :

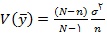
 در رابطه ی فوق    بوده و واریانس جامعه نامیده می شود.

 محاسبه ی واریانس میانگین جامعه به دلیل آن که عملاً محاسبه ی   (تغییرات جامعه) امکان پذیر نیست، میسر نمی باشد. از این روی از برآورد واریانس میانگین جامعه که به صورت زیر تعریف می شود استفاده می کنیم،

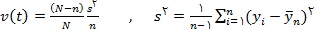
 تغییرات نمونه نامیده می شود.

1-1- تعیین حجم نمونه برای برآورد میانگین جامعه

 در انتخاب حجم نمونه باید به دو نکته توجه نمود، اول آن که اگر حجم نمونه خیلی بزرگ باشد منجر به صرف هزینه های زیاد می شود و از طرف دیگر اگر حجم نمونه کم باشد برآوردهای نامناسبی را نتیجه می دهد.

یک راه برای برآورد حجم نمونه استفاده از کران خطای برآورد (B) می باشد. در این روش حجم نمونه با استفاده از رابطه ی زیر بدست می آید:

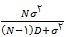
در این رابطه  بوده و  نیز تغییرات جامعه را بیان می کند.

از آنجایی که محاسبه ی تغییرات جامعه اغلب امکان پذیر نیست، در رابطه ی فوق از  (تغییرات نمونه) که با استفاده از یک نمونه ی اولیه و یا با توجه به نمونه گیری های مشابه قبلی بدست آمده است، استفاده می کنیم. گاه نیز براساس این قاعده ی تجربی که دامنه حدوداً 4 برابر انحراف معیار است، واریانس جامعه تخمین زده می شود . یعنی   که در آن R دامنه تغییرات متغیر مورد بررسی می باشد.

2- برآورد نسبت (درصد) جامعه

گاه محققی که یک بررسی نمونه ای را انجام می دهد، به نسبت عناصری از جمعیت که دارای صفت خاصی هستند علاقمند است. به طور مثال ممکن است برای یک گروه بازاریابی دانستن نسبت فروش کل یک فرآورده ی بخصوص که در تهیه ی جیره ی غذایی روزانه به کار می رود، اهمیت داشته باشد. و یا به منظور ارزیابی برنامه های تلویزیونی اغلب نسبت بینندگانی که یک برنامه ی خاص را مشاهده می کنند، برآورد می شود.

 همانطور که مشاهده می کنید تمام مثال های از این نوع دارای یکی از مشخصات آزمایش دوجمله ای هستند. یعنی یک مشاهده یا به دسته ی مورد نظر تعلق دارد یا ندارد. به این ترتیب اگر i امین عنصر نمونه خاصیت مورد نظر محقق را نداشته باشد،   و در غیر اینصورت  قرار می دهیم. بنابراین تعداد کل عناصری که ویژگی مفروض را در نمونه ای به حجم n دارا هستند برابر است با    و برای برآورد نسبت کسانی در جامعه که دارای ویژگی هستند از

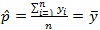
استفاده می کنیم.

 برآورد واریانس این برآوردگر به صورت زیر تعریف می شود :

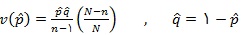
1-2- حجم نمونه

 در این حالت نیز حجم نمونه مشابه قبل محاسبه می شود،

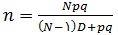
در عمل مقدار p معلوم نیست و از مقدار برآورد شده ی ، که باز هم از مطالعات مشابه قبل و یا با استفاده از یک نمونه ی اولیه حاصل شده است، در رابطه ی فوق استفاده می شود. در صورتی که هیچ اطلاعی در باره ی p در دست نباشد ، p=0.5 در نظر گرفته می شود. با این فرض احتمالاً حجم نمونه بزرگتر از مقدار واقعی مورد نیاز محاسبه می شود.

منبع: مقدمه ای بر بررسی های نمونه ای ، نوشته ی شیفر و مندنهال . ترجمه ی دکتر ارقامی ، دکتر بزرگنیا و دکتر سنجری . انتشارات دانشگاه فردوسی مشهد.

براي مشاهده ساير مقاله هاي تحليل آماري اين وب سايت بر لينک زير کليک نماييد: صفحه مقاله هاي تحليل آماري

3- سوالات احتمالی در خصوص نمونه گیری تصادفی ساده

بسته نرم افزاري تعيين حجم نمونه با فرمول کوکران

پژوهشگر گرامي مي توانيد تنها با چند کليک نرم افزار اکسلي کوچک اما پرکاربردي را خريداري نماييد که بر اساس فرمول کوکران حجم نمونه براي پژوهش شما را محاسبه نمايد و تمامي مستندات توضيحي لازم در اين خصوص را نيز دريافت نماييد:  بسته کامل تعیین حجم نمونه با فرمول کوکران