آنالیز واریانس چیست؟
از جمله سؤالات متداول که که با اجرای یک طرح پژوهشی مایل هستیم به آن پاسخ داده شود، وجود یا عدم وجود تفاوت معنی دار بین دو یا چند سطح متغیر پاسخ می باشد.
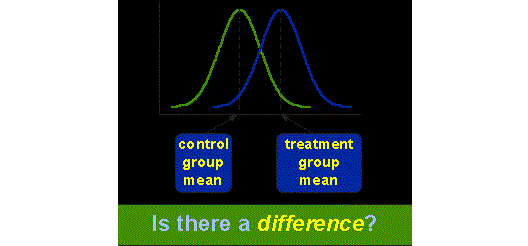
در حالتی که هدف مقایسه میانگین در دو گروه باشد مانند مقایسه ی وضعیت بهبود بیماران در دو گروه کسانی که از دارونما استفاده می کنند و کسانی که داروی خاصی را دریافت می کنند و یا مقایسه کشش نوعی سیمان که با دو فرمول مختلف بدست آمده است، آزمایش دارای یک عامل بوده که در دو سطح مختلف اندازه گیری می شود و با توجه به شرایط موجود به کمک آزمون های z نرمال یا t استودنت قابل بررسی می باشد.
اما بسیاری از این نوع آزمایش ها بیش از دو سطح یک عامل را شامل می شوند، در چنین حالتی یک ابزار مقایسه سطوح (تیمارهای) یک عامل استفاده از تحلیل واریانس یا ANOVA می باشد.
مثال
برای مثال فرض کنید یک مهندس برای بهبود محصول مایل است مقاومت کششی یک نخ مصنوعی جدید را حداکثر نماید. از طرفی وی می داند که درصد پنبه ی نخ در میزان مقاومت آن مؤثراست و از آنجایی که میزان پنبه در نخ بایستی بین 10 تا 40 درصد باشد، محقق در هریک ازسطوح 15 ،20، 25، 30 و 35 درصد پنبه، میزان مقاومت کششی نخ را برای 5 مشاهده اندازه گیری می کند. حال برای بررسی درصدهای مختلف پنبه بایستی تفاوت های بین میانگین مقاومت ها را برای هر پنج سطح عامل درصد پنبه، آزمون کنیم.
ممکن تصور شود که با انجام آزمون t برای تمام جفت میانگین های ممکن این مسئله قابل حل باشد، در حالی که این روش نمی تواند یک راه حل صحیح باشد زیرا منجر به افزایش خطا خواهد شد.
فرض کنید در مثال بالا بخواهیم تمام 10 جفت آزمون ممکن را برای مقایسه میانگین های دوبه دو داشته باشیم، به این ترتیب با فرض مستقل بودن تمام این آزمون ها و این که احتمال این که فرض صفر (برابری میانگین 5 گروه ) به درستی پذیرفته شود برابر 95% باشد، حال آنکه احتمال پذیرش صحیح فرض صفر مبنی بر برابری همزمان تمام جفت میانگین ها برابر 0.6 خواهد بود و خطای نوع اول در این حالت برابر 0.4 می شود که بسیار زیاد است.
(آنالیز) تحلیل واریانس



منبع :خلاصه ای بر طرح و تجزیه آزمایش ها . نوشته داگلاس سی. مونت گومری ترجمه محمد رضا دهقانی نشر پلک.
براي مشاهده ساير مقاله هاي تحليل آماري اين وب سايت بر لينک زير کليک نماييد: صفحه مقاله هاي تحليل آماري
قبول سفارش انجام تحلیل واریانس
آمادگی داریم تحلیل واریانس پایان نامه یا مقاله isi شما را در زمان مناسب به انجام برسانیم.
ضمنا اگر سوالی در خصوص روش آنالیز واریانس دارید، در بخش دیدگاه در پایین همین صفحه درج تا به آن پاسخ دهیم. از طریق ایمیل تان از پاسخ ما به سوالتان مطلع خواهید شد.





10 دیدگاه. همین الان خارج شوید
سلام آقای مهندس وقتتان بخیر. آیا بعد از نرمال کردن داده ها توسط sqrt یا log 10 نیاز است که دوباره امتحان کنیم که داده ها نرمال شده اند؟ چون بعد از انجام مراحل باز نرمال نیستند. چطور داده ها رو نرمال کنم؟
آیا آنالیز واریانس آنوا را میتوان روی داده های رتبه ای و غیرنرمال انجام داد؟ از یاریتان سپاسگذارم.
سلام. بله بعد از هر تبدیلی لازم است کنترل کنید که آیا داده ها نرمال شدند یا خیر. با حذف داده های پرت و آزمون و خطا بر روی تبدیل های مختلف داده ها را نرمال کنید.
برای آنالیز واریانس باید داده ها نرمال باشند خصوصا متغیر وابسته.
سلام آقای مهندس بسیار ممنونم از پاسخگوئیتان .داده های پرت حذف شدند اما باز نرمال نیستند در بعضی ستونها داده هایی دارم که واقعی اند و ارزشمند هستند مثل داده مربوط به رشد ارتفاعی نهالهایی که زودتر از همه سبز شده بودند با حذفشان به نتیجه آزمایش لطمه نمیزنم؟ راه دیگری برای نرمالسازی نیست تابع دیگری بجز log و sqrt نداریم؟؟میخواستم بین رشد ارتفاعی (کمی) میانگین رشد جوانه(کمی) و زمان ظهور (رتبه ای) از آنالیز واریانس چندطرفه استفاده کنم اما ستونهایم نرمال نمیشوند. به نظر شما برای اینکه رابطه دو متغیر زمان ظهور و رشد جوانه روی متغیر وابسته رشد ارتفاعی را بسنجم از چه آزمونی استفاده کنم بهتر است با توجه به اینکه ستون رشد ارتفاعیم نرمال نمیشود. بسیار از شما ممنونم.
سلام. در حذف داده های پرت باید با احتیاط اقدام کنید.
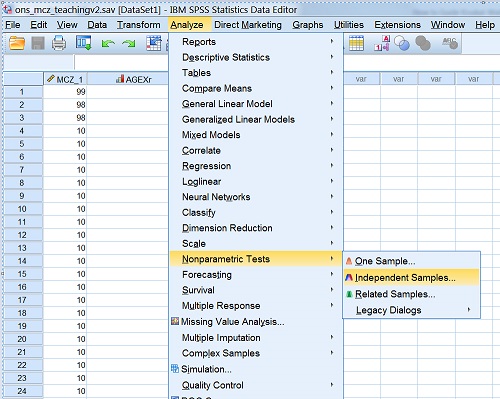
اگر دیدید نرمال نشدند، از معادل ناپارامتری آنالیز واریانس یعنی آزمون کروسکال والیس استفاده کنید.
سلام. وقت بخیر. برای انجام تحلیل واریانس دو طرفه برای ازمون فرض ها میشه از نرم افزار eviews هم استفاده کرد؟ یا بهتر هست از spss استفاده بشه؟ با توجه به اینکه داده ها به صورت پانل هست.
سلام. اگر داده ها پانل هست حتما بابستی از نرم افزار ایویوز استفاده نمایید. در spss نمی توان داده های پانل را تحلیل نمود. در سایت آموزش نرم افزار EViews و مبحث پانل دیتا: http://www.eviews-iran.ir که سایت دیگر ماست، ویدئوهای آموزشی بسیار خوبی در زمینه رگرسیون داده های پانلی وجود دارد.
سلام
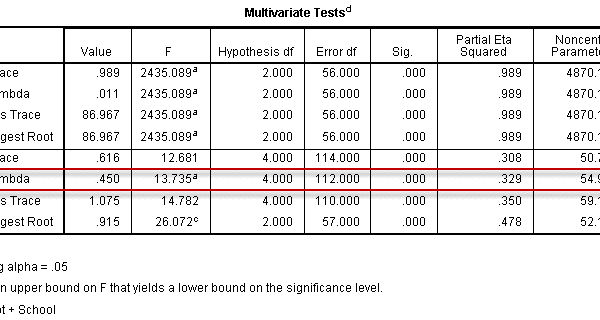
اگر پیش فرض های تحلیل واریانس چند متغیری رعایت نشود.
هماننده آزمون باکس و آزمون لوین در این صورت باید از چه باید کرد؟
و یا اگر آزمون باکس معنادار شد ولی آزمون لوین معنادار نشد و یا در کل برعکس آن اتفاق افتاد چه باید کرد؟
سلام. باید با کمی اغماض پیش فرض های تحلیل واریانس را پذیرفت (مثلا سطح معناداری 0.0001 برای آزمون باکس) وگرنه باید آزمون ناپارامتری برای تک تک متغیرها انجام داد
سلام
وقت بخير
ممنون از مطالب مفيدتون، اگه در اين حالت، متغير پاسخ كمي نباشه و طبقه بندي باشه به جاي آناليز واريانس يا آناليز كواريانس از چه آزموني ميشه استفاده كرد؟
سلام. آزمون کای دو (جدول توافقی)