از جمله روش های انتخاب متغیر در اجرای یک رگرسیون، استفاده از روش های رگرسیون گام به گام می باشد که در نرم افزار spss نيز قابل انجام مي باشد.
برای این منظور در سه روش مختلف متغیرها یک به یک به الگو وارد می شوند و یا از آن حذف می شوند. این روش ها عبارتند از : انتخاب پیشرو، حذف پسرو و الگوریتم افرویمسان.
در زير به توضيح هر کدام از روش ها مي پردازيم.
انتخاب پیشرو
ایده ابتدایی این روش بسیار ساده است. اگر k متغیر پیشگو (مستقل) داشته باشیم، k الگوی رگرسیون خطی ساده را برای هر یک از پیشگوها محاسبه می کنیم. الگویی که بیشترین مقدار F (آماره آزمون معنی داری الگوی رگرسیون) را داشته باشد، می تواند انتخابی مناسب در این مرحله از انتخاب متغیرها باشد. مقدار F به صورت زیر حاصل می شود :
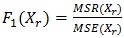
که در آن
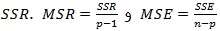
مجموع مربعات رگرسیون می باشد.
این مقدار میزان تغییراتی از متغیر پاسخ را که توسط مدل برازش شده تبیین می شود، نشان می دهد. مجموع مربعات رگرسیون دارای p-1 درجه آزادی می باشد.
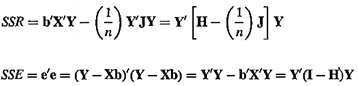
ماتریس H به شکل مقابل تعریف می شود :
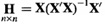
SSE نیز میزان تغییراتی از متغیر پاسخ که توسط مدل رگرسیون بیان نمی شود را بیان می کند. این عبارت دارای n-p درجه ی آزادی است.
توجه کنید که چون در هر مرحله تنها یک متغیر در نظر گرفته می شود p=1 می باشد. متغیری با بیشترین مقدار F1 متغیر انتخاب شده در این فرآیند است.
اکنون این روش را که متغیرهای انتخاب شده در مراحل قبلی همیشه بخشی از الگو هستند را تکرار می کنیم. در مرحله دوم علاوه بر متغیر انتخاب شده در مرحله اول هریک از k-1 متغیر باقی مانده را یک به یک وارد مدل می کنیم و مقدار آماره F را به صورت زیر محاسبه می نماییم :
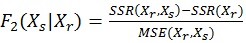
متغیری که بیشترین مقدار F2 را داشته باشد با این روش انتخاب می کنیم. این فرآیند تا زمانی که انتخاب متغیرها پایان یابد ادامه می یابد.
چند معیار برای پایان دادن به روش انتخاب پیشرو وجود دارد. معمولا مقدار F با مقدار F آزمون حاصل ازجدول توزیع فیشر مقایسه می شود. انتخاب متغیر تا زمانی ادامه می باشد که F بیشینه انتخاب شده از مقدار بحرانی جدول بزرگتر باشد. البته روش بررسی همبستگی های جزئی R2 یا بالاترین مقدار آماره t برای ضرایب به جای بیشترین مقدار F، نیزمی توانند مورد استفاده قرار گیرند.
حذف پسرو
این روش برخلاف روش انتخاب پیشرو با الگوی کامل یعنی ورود تمام متغیرها به مدل شروع می شود.
دلیل حذف متغیری مانند Xr از الگو این است که بعد از حذف متغیر تنها زیان کمی به برازش وارد می آید. آماره Fk محاسبه شده به صورت زیر است :
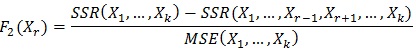
برای هریک از متغیرهای الگوی کامل Fk محاسبه می کنیم و متغیری که کمترین مقدار Fk را دارد از الگو حذف می نماییم. این روش پس از حذف اولین متغیر ادامه می یابد. مانند قبل یک مقدار بحرانی F را برای متوقف کردن این الگو انتخاب می کنیم. الگو تا زمانی ادامه می یابد که مقدار F کمینه در هر مرحله از این مقدار بحرانی بیشتر باشد.
الگوریتم افرویمسان
این الگوریتم ترکیبی از انتخاب پیشرو و حذف پسرو است. یک عیب آشکار روشهای گام به گام معرفی شده، ناتوانی آن ها در اصلاح تصمیماتی است که به وسیله روش ها انجام می شود. یعنی حذف یک متغیر بعد از اینکه با انتخاب پیشرو انتخاب شد و یا برگرداندن یک متغیر بعد از این که با حذف پسرو حذف شده است.
الگوریتم پیشنهاد شده بوسیله افرویمسان بر این معایب چیره می شود. مانند انتخاب پیشرو این روش با ورود متغیری که بیشترین مقدار F1 را حاصل می کند و آزمون F را برقرار می سازد، شروع می شود. به همین ترتیب متغیر دوم انتخاب می شود، اما اکنون این روش بررسی می کند که هر یک از متغیرهایی که تاکنون وارد شده اند را با آزمون حذفی می توان حذف کرد یا خیر؟ به طور کلی بعد از این که یک متغیر با آزمون F ورودی انتخاب شد، این روش سعی می کند متغیرهایی را که دیگر برای برازش الگوی مناسب با استفاده از آزمون F حذفی لازم نیستند، را حذف کند.
بنابراین در اینجا نیاز به دو مقدار بحرانی F یکی برای آزمون F ورودی و دیگری برای آزمون F حذفی وجود دارد.
منبع : تحلیل رگرسیون در علوم اجتماعی / نوشته ی الکساندر ون آی و کریستف اسکاستر / ترجمه دکتر حسینعلی نیرومند/ انتشارات دانشگاه فردوسی مشهد.