1- نمونه گیری خوشه ای دو مرحله ای چیست؟
نمونه گیری گروهی دو مرحله ای در واقع تعمیمی از مفهوم نمونه گیری خوشه ای است. یک خوشه عمدتاً مجموعه ای طبیعی یا مناسب از اعضا است، مانند بلوک هایی از خانوارها یا کارتون هایی از لامپ های تولید شده. هر خوشه ی مورد بررسی یا دارای تعداد اعضایی است بیش از آنچه که بتوان همه ی آن ها را مورد بررسی قرار داد و یا دارای اعضایی است که آن قدر مشابه هستند که اندازه گیری تعداد کمی از آن ها اطلاعاتی درباره ی تمام خوشه در اختیار ما قرار می دهد.
در هریک از موارد ذکر شده، پژوهشگر می تواند یک نمونه ی احتمالی از خوشه ها برگزیده و سپس یک نمونه ی احتمالی از اعضای درون هر خوشه انتخاب نماید. به این ترتیب یک نمونه ی خوشه ای دومرحله ای حاصل می شود.
نمونه گیری احتمالی که در هر مرحله انجام می شود می تواند به کمک روش های مختلف نمونه گیری انجام شود. به دلیل کاربرد بیشتر نمونه گیری تصادفی ساده در ادامه نمونه گیری خوشه ای دو مرحله ای را با فرض آن که در هر مرحله نمونه ی مورد نظر با استفاه از روش تصادفی ساده حاصل شود ، بررسی می کنیم.
2- چند مثال کاربردی
1- یک بررسی ملی از نظرات دانشجویان، به وسیله انتخاب یک نمونه تصادفی ساده از دانشگاه های کشور و سپس انتخاب یک نمونه تصادفی ساده از دانشجویان هر دانشگاه انجام می شود. بنابراین هر دانشگاه متناظر با یک خوشه از دانشجویان است.
2- مقدار کل حساب های قابل وصول برای یک فروشگاه زنجیره ای را می توان ابتدا به وسیله ی گرفتن یک نمونه ی تصادفی ساده از فروشگاه ها و سپس انتخاب یک نمونه تصادفی ساده از حساب های هر کدام برآورد نمود. به این ترتیب هر فروشگاه زنجیره ای یک خوشه از حساب ها را فراهم می کند.
3- نمونه گیری برای اهداف کنترل کیفیت نیز اغلب شامل دو مرحله (یا بیشتر) است. برای مثال زمانی که یک بازرس از محصولات بسته بندی شده مانند غذای یخ زده نمونه گیری می کند، معمولا از میان کارتون ها تعدادی را انتخاب کرده و سپس از بسته های درون کارتون ها نمونه گیری می کند.
4- زمانی که نمونه گیری مستلزم وارسی مولفه های محصول ، مانند اندازه گیری ضخامت صفحه باطریهای اتومبیل است ، یک روند نمونه گیری عبارت است از نمونه برداری از برخی فرآورده ها (باطری ها) و سپس نمونه برداری از مولفه های (ضخامت) درون این فرآورده ها می باشد.
3- چگونه یک نمونه خوشه ای دو مرحله ای انتخاب کنیم؟
مهمترین مسئله در برگزیدن یک نمونه ی خوشه ای دو مرحله ای انتخاب خوشه های مناسب است. دو شرط اصلی در انتخاب خوشه ها مجاورت جغرافیایی اعضای درون یک خوشه و بزرگی خوشه ها برای اجرای راحت تر طرح ، می باشد.
همانطور که اشاره شد انتخاب خوشه ها همچنین بستگی به آن دارد که آیا ما می خواهیم تعداد کمی خوشه با اعضای زیاد در هر یک داشته باشیم و یا قصد داریم تعداد خوشه ها زیاد بوده و در عوض تعداد اعضای کمی در هرخوشه قرار گرفته باشد. خوشه های بزرگ به داشتن اعضای نامتجانس (متفاوت) تمایل دارند و بنابراین نمونه ی بزرگی از هر کدام برای دست یابی به برآوردهای دقیقی از پارامترهای جامعه لازم است. در مقابل خوشه های کوچک اغلب دارای اعضای نسبتاً متجانس هستند ، در این حالت با انتخاب نمونه ی کوچکی از هر خوشه اطلاعات دقیقی درباره ی مشخصه های آن خوشه می توان فراهم نمود.
برای مثال نظرسنجی از دانشجویان دانشگاه های مختلف را درنظر بگیرید. اگر دانشجویان درون هر دانشگاه عقیده ی مشابهی در مورد سوال مورد نظر داشته باشند اما عقاید از دانشگاهی به دانشگاه دیگر بسیار متفاوت باشد، در آن صورت نمونه باید شامل گروه های کوچکی از تعداد زیادی دانشگاه باشد. یعنی تعداد خوشه ها زیاد بوده و تعداد نمونه ی انتخابی از هریک اندک باشد.
در مقابل اگر عقاید در هر دانشگاه بسیار متغیر باشد ، بررسی باید شامل تعداد کمی دانشگاه و نمونه ی بزرگی از هر یک از دانشگاه های انتخابی باشد.
به طور خلاصه برای اجرای نمونه گیری خوشه ای دو مرحله ای، ابتدا چارچوبی از کلیه ی خوشه ها در جامعه فراهم می آوریم، سپس یک نمونه ی تصادفی ساده از خوشه ها انتخاب می کنیم. در ادامه چارچوب های کلیه ی اعضای هر خوشه ی انتخاب شده را فهرست کرده ، یک نمونه ی تصادفی از اعضای هر یک از این چارچوب ها بر می گزینیم.
4- برآوردیابی میانگین جامعه
از جمله مهمترین اهداف در هر طرح نمونه گیری بدست آوردن برآوردی از میانگین کل جامعه می باشد.در روش نمونه گیری خوشه ای دو مرحله ای نیز برآوردگر نااریب برای میانگین جامعه به صورت زیر تعریف می شود :
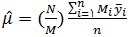
در این رابطه N تعداد خوشه ها در جامعه ، n تعداد خوشه های انتخابی در یک نمونه ی تصادفی ساده،
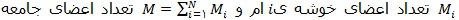
می باشند. لازم به ذکر است که Mi y̅i در واقع برآوردی برای مقدار کل خوشه ی iام است.
برآورد واریانس برآوردگر معرفی شده µ عبارت است از :
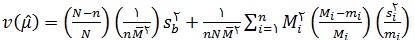
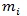
در رابطه ی بالا mi تعداد اعضای انتخاب شده در یک نمونه ی تصادفی ساده از گروه i ام است. همچنین داریم :
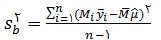
و
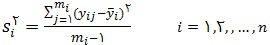
5- برآورد نسبی میانگین جامعه
برآوردگر معرفی شده µ به نعداد کل اعضای جامعه (M) بستگی دارد . از آنجایی که این مقدار اغلب نامعلوم است ، با کمک داده های نمونه، برآوردگر
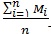
را برای آن در نظر می گیریم . به این ترتیب برآوردگر نسبی جامعه به صورت زیر تعریف می شود:
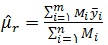
واریانس این برآوردگر نیز به صورت زیر تغییر می یابد،
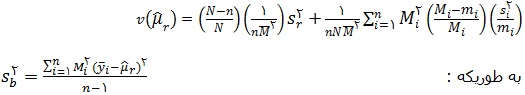
برآوردگر µr اریب است ولی زمانی که n بزرگ باشد می توان از اریبی آن چشم پوشی کرد.
منبع : مقدمه ای بربررسی های نمونه ای . نوشته ی شیفر و مندنهال. ترجمه ی دکتر ارقامی ، دکتر بزرگنیا و دکتر سنجری . انتشارات دانشگاه فردوسی مشهد.





3 دیدگاه. همین الان خارج شوید
لطفا درباره کو واریانس و تحلیل آن(ANCOVA) همراه با ذکر یکی دو نمونه،مثال توضیح بدهید. خیلی از شما سپاسگزارم
سلام من میخواستم برای یک پروژه ، نمونه گیری خوشه ای انجام بدم آیا نرم افزاری هست که هم زمان کارایی بین cluster , srsw رو با هم برای یک سری داده مقایسه بتونم بکنم باهاش و خودش طوری خوشه هارو دسته بندی کنه که واریانس بین خوشه ها کم و درون خوشه ها زیاد باشه؟
سلام
سوال خیلی فنی است. نمیدانم. معمولا برای این کارهای خاص، نرم افزار R به کار می رود.