زمانی که در یک تحقیق، هدف مقایسه یک متغیر در دو وضعیت متفاوت باشد و در صورت عدم برقراری فرض نرمال بودن نمونه می توان از آزمون های ناپارامتری مانند آزمون علامت، آزمون ویلکاکسون و آزمون مک نمار برای مقایسه دو گروه وابسته استفاده نمود. در این مطلب به معرفی آزمون ویلکاکسون پرداخته می شود.
در آزمون ویلکاکسون نیز مانند آزمون علامت الزامی در مورد نوع توزیع متغیر مورد نظر وجود ندارد اما مقادیر متغیر مورد نظر باید پیوستگی داشته و مقیاس آن از نوع ترتیبی باشد. بعبارت دیگر اجرای این آزمون برای متغیرهایی که دارای مقوله های محدودی هستند امکان پذیر نیست.
توجه : در آزمون علامت تنها علائم مثبت و منفی به کار گرفته می شود در حالیکه یک واحد ممکن است 1 واحد اختلاف داشته باشد و واحد دیگر 10 واحد. آزمون ویلکاکسون علاوه بر در نظر گرفتن مثبت یا منفی بودن داده ها، مقدار تفاوت آن ها را نیز در نظر می گیرد و چون اطلاعات بیشتری را مورد استفاده قرار می دهد نتایج دقیقتری از آزمون علامت ارائه می دهد. به مثال زیر توجه کنید.
مثال:
فرض کنید نمره اطلاعات عمومی افراد در دو وضعیت قبل و بعد از شرکت در یک دوره آموزشی اندازه گیری شده باشد. می خواهیم بدانیم آیا دوره آموزشی سطح اطلاعات عمومی افراد را افزایش داده است یا خیر؟
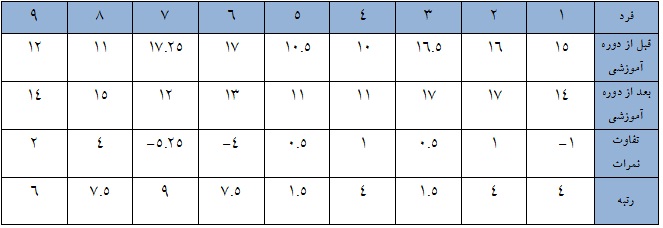
در این جدول ابتدا تفاوت بین نمرات حساب شده و سپس قدر مطلق این تفاوت ها مبتای محاسبه رتبه قرار داده شده است. فرد شماره 3 و 5 با داشتن تفاوت نمره 0.5 کمترین تفاوت را در بین نمونه ها دارند و بنابراین میانگین رتبه های 1 و 2 (1.5) به این دو تعلق می گیرد و به همین ترتیب سایر نمونه ها نیز رتبه بندی می شوند. حال محقق می تواند با توجه به زوج هایی که افزایش نمره و یا کاهش نمره داشته اند به جمع رتبه ها پرداخته و از آماره زیر برای آزمون مورد نظر استفاده نمود.
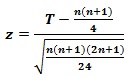
n حجم نمونه مورد استفاده و T مجموع رتبه های افرادی است که افزایش نمره (یا کاهش نمره) داشته اند.
آماره ی حاصل با توجه به یک طرفه یا دو طرفه بودن فرض مقابل مورد بررسی قرار می گیرد.در صورتی که حجم نمونه ها کوچک باشد این آماره با مقدار حاصل از جدول ویلکاکسون مقایسه می شود و در صورت بزرگ بودن حجم نمونه از توزیع نرمال برای رد یا پذیرش فرض صفر استفاده می نماییم.
نکته :
1. مقدار حاصل از آماره ویلکاکسون به ازای استفاده از مجموع رتبه های مثبت یا منفی برابر می باشد و تنها تفاوت این آماره ها در علامت آن ها است. (مقدار آماره به ازای رتبه های منفی دارای علامت منفی است).
2. در محاسبه n حجم نمونه تعداد افرادی که نمره ثابتی در دو وضعیت داشته اند از حجم کل نمونه حذف می شوند.
منبع : آمار ناپارامتریک ، نوشته سید یعقوب حسینی ، انتشارات دانشگاه علامه طباطبایی.




4 دیدگاه. همین الان خارج شوید
با سلام
خداوند به حق غدیر، بهترینها در دنیا و آخرت نصبتان گردد. اجرکم عندالله
سلام. متشکرم و بسیار تشکر می کنم از انرژی مثبتی که به ما دادید.
سلام. بسیار ممنون از مطلب کاربردی شما. من آزمون فریدمن رو انجام دادم و مقدار پی معنادار شد (۰.۰۴۱) اما در ازمون پست هاک ویلکاکسون بین هیچ کدام از زمان های درمان (جلسه ۱ و ۲ و ۳) مقدار پی معنادار نبود! این چطور ممکن هست!
و سوال دوم این که اگر فریدمن و یا انوا با اندازه گیری مکرر معنادار نبودن دیگر نیازی به گرفتن ازمون پست هاک نیست؟
ممنون از لطف شما
سلام
آزمون فریدمن آزمونی متفاوت با تحلیلی متفاوت نسبت به پست هاک ویلکاکسون است و قابل قیاس نیستند.
سوال دوم: اگر در آنوا شاهد معنی داری نبودید، دیگر گرفتن آزمون های پست هاک معنایی ندارد. زیرا از ریشه تفاوت معنادار داشتن رد شده است و لذا مقایسه معنایی ندارد.