برای (مقایسه چند گروه داده کمی وابسته)- با ذکر مثال
اگر در انجام طرح آزمایش بلوکی کاملا تصادفی، برخی مشاهدات مربوط به جدول به دلایلی چون هزینه بالا، نیاز به صرف زمان زیاد و … جمع آوری نشوند، مقادیر آن خانه ها گمشده به حساب می آید. طرح متناظر با این وضعیت را ناقص می نامند.
در این نوشتار آزمون یکسانی میانه ها را در سطوح مختلف تیمارهای این طرح بررسی می کنیم. این آزمون یک آزمون ناپارامتری یا توزیع آزاد است.
فرض صفر بیانگر تساوی اثر k سطح عامل مورد مورد نظر است.
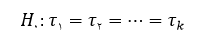
در مقابل فرض H_1 می گوید که حداقل یکی از تساوی های فرض صفر برقرار نیست.
اگر تعداد مشاهدات بی پاسخ (اندازه گیری نشده یا گمشده) در تمامی بلوک ها یکسان باشد، طرح بلوک ناقص را متعادل می نامیم. در این طرح فرض می شود که
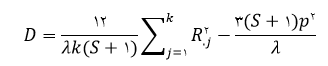
تحت فرض H_0 و به شرط وجود مقادیر بزرگ b آماره D دارای توزیع تقریبی کای دو با k-1 درجه آزادی است.
در سطح خطای α درصد، چنانچه آماره D بزرگتر از مقدار حاصل از جدول توزیع کای دو با k-1 درجه آزادی باشد، فرض صفر تأیید نمی شود.
در ادامه ماتریس داده ها در یک طرح بلوکی را مشاهده می کنید:
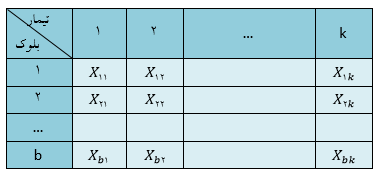
مثال
اثر 7 ماده شیمیایی در 7روز مختلف بر روی عملکرد یک فرآیند شیمیایی بررسی شده است. چون هر آزمایشگر در هر روز تنها قادر بوده است 3 ماده شیمیایی را آزمایش کند، از یک طرح بلوکی ناقص استفاده شده است. با توجه به داده های جمع آوری شده مقدار اماره D برابر 7.71 حاصل می شود. با مقایسه مقدار D با مقدار حاصل از جدول توزیع کای دو با (1-7) درجه آزادی و در سطح خطای 0.05، مقدار D کوچکتر از مقدار حاصل از جدول بوده و فرض صفر مبنی بر یکسانی اثر نوع مواد شیمیایی رد نمی شود.
منبع : مقدمه ای بر روش های آماری ناپارامتری / نوشته : اکبر گلدسته / انتشارات جهاد دانشگاهی / 1390.
ساير منابع مرتبط با آزمونهاي آماري :
در خصوص آزمونهاي آماري مي توانيد از مطالب وب سايت ديگر اين شرکت آماری نيز استفاده نماييد: آزمون هاي آماري




1 دیدگاه. همین الان خارج شوید
سلام. لطفا سوالات و نظرات خود در خصوص اين مطلب را در همين بخش ديدگاه مطرح نماييد. از طريق ايميل از پاسخ ما مطلع خواهيد شد.
براي جستجو در ميان کامنت ها از Ctrl + f استفاده نماييد.